Formules matricielles

Le calcul matriciel est un outil à la fois très puissant et très méconnu.

Une matrice est un tableau de chiffre qui est considéré par Excel comme une entité indissociable.
Une formule matricielle s'écrit donc souvent (pas toujours) sur plusieurs cellules à la fois.
Par exemple, sélectionner la plage A1:A5. Inscrire dans la barre de formule ={3;5;2;4;8}.
Les accolades indiquent une matrice, les points-virgules signifient matrice verticale.
Valider la formule, non pas par Entrée (qui ne valide qu'une cellule), mais par CTRL+MAJ+Entrée.

 


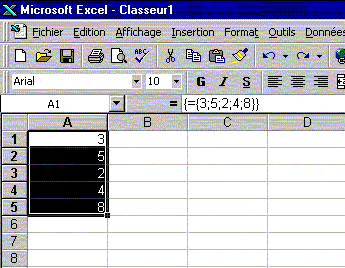
Excel inscrit, en colonne, les éléments de la matrice.
La formule qui apparaît dans la barre de formules est entourée d'accolades (automatiquement ajoutées par Excel).
Il est impossible de modifier séparément une des cellules de la matrice.


De la même façon, ={9\6\7}, validé par CTRL+MAJ+Entrée, va renvoyer une matrice horizontale,
et ={9\6\7;3\5\4} une matrice à deux lignes et trois colonnes
(attention, dans certaines configurations, les antislashes doivent être remplacés par des points).

Toutes les cellules de la matrice sont liées entre elles. Pour modifier la matrice, il faut
  • soit sélectionner l'ensemble de la matrice (ou bien une plage plus grande) et modifier la formule dans la barre de cellule avant de valider par CTRL+MAJ+Entrée,
  • soit casser la matrice en n'en conservant que les valeurs numériques : sélectionner la matrice, Edition / Copier / Edition / Collage spécial / Valeurs,
  • soit encore casser la matrice en recopiant la formule dans chaque cellule : sélectionner la matrice, positionner le curseur dans la barre de formules, valider par CTRL+Entrée.

Remarques :

Pour sélectionner l'ensemble d'une matrice (avant de la modifier par exemple), sélectionner l'une des cellules de la matrice et taper CTRL+/ . Ce raccourci est très utile pour sélectionner les grandes matrices (il remplace Edition / Atteindre / Cellules / Matrice en cours).
La validation par CTRL+Entrée permet de recopier la même formule dans une plage Excel. Utile pour éviter des recopies vers le bas ou vers la droite.
 

Opérations sur les matrices

Le calcul matriciel permet de faire des opérations entre matrices.

Le signe égal permet de recopier une plage de données d'un bloc.
On peut, après avoir sélectionné une plage de 8 cellules, écrire =A1:B4 et valider par CTRL+MAJ+Entrée
Plus intéressant, on peut faire référence à une plage nommée. Si la plage A1:B4 est nommée plage1, on peut sélectionner une plage de la même taille et inscrire =plage1 puis valider par CTRL+MAJ+Entrée.
Cette méthode est très utile pour transférer des blocs de données, notamment entre deux fichiers (une seule liaison entre les fichier pour transférer un grand nombre de données).
La formule de la matrice ressemble à {='C:\mes documents\[fichier.xls]Feuil1'!zone1}. Il est généralement inutile de taper le chemin d'accès, puisqu'on peut sélectionner la zone zone1 à la souris.
On peut multiplier ou diviser une matrice par un nombre en écrivant :
=5*A1:B4 (validation par CTRL+MAJ+Entrée).
L'exemple ci-dessous indique comment convertir en Euros un tableau de données en Francs.


La formule de la matrice est simplement
{=C3:C7/6.55957}.
On aurait pu insérer le tableau converti sur une autre feuille ou bien dans un autre classeur.

 
On peut également faire la somme (ou la différence, ou le produit…) de deux matrices de taille identique : {=C3:D7+E5:F9}
Dans l'exemple ci-dessous, c'est l'écart relatif entre deux tableaux qui est calculé :


 
Formule matricielle :
{=F4:G8/D4:E8-1}

 
Remarques :
- Si on multiplie une matrice par une cellule, on multiplie chaque cellule de la matrice par la cellule.
Si on multiplie une matrice par une matrice à une seule colonne, on multiplie chaque colonne de la première par la seconde.
- On peut utiliser la fonction TRANSPOSE pour transposer une matrice.
- Les fonctions agissant sur des plages, comme SOMME, MOYENNE, MAX… peuvent être utilisées indifféremment avec des plages de cellules ou avec des matrices. Elles renvoient des nombres et non des matrices
{=MAX(D4:E8)} renvoie la même valeur que =MAX(D4:E8).
- Les fonctions DECALER, INDEX ou EQUIV (cf. fonctions de références) peuvent par contre renvoyer des matrices.
- utile parfois, la fonction PRODUITMAT permet de faire des produits de matrices. On peut notamment l'utiliser pour calculer un vecteur contenant la somme des éléments de chaque colonne d'une matrice :
Pour calculer le vecteur contenant la somme de toutes les colonnes de C5:E9, on peut sélectionner trois cellules en ligne, écrire la formule matricielle =PRODUITMAT({1\1\1\1\1};C5:E9) et valider par CTRL+MAJ+Entrée
On écrira de même =PRODUITMAT(C5:E9;{1;1;1}) en matriciel dans un vecteur de trois cellules en colonne pour faire la somme des lignes.
Pour éviter de taper une série de 1, on peut utiliser une matrice horizontale comme =1+0*COLONNE(A1:D1) qui va renvoyer 4 fois 1.
Ce qui permet de calculer la matrice verticale somme des lignes d'une plage nommée "plage" :
=PRODUITMAT(plage;1+0*TRANSPOSE(COLONNE(plage)))
ou la somme des colonnes (vecteur horizontal) de la même plage :
=PRODUITMAT(1+0*TRANSPOSE(LIGNE(plage));plage)
(Formules élaborées avec l'aide de Daniel Maher).
 

Les calculs conditionnels

C'est dans les calculs complexes mettant en jeu des opérations sous conditions sur de grandes bases de données que les formules matricielles prennent tout leur intérêt.
Par exemple, dans une base de données de personnel, calculer le salaire moyen des femmes d'age compris entre 35 et 42 ans et ayant plus de 12 ans d'ancienneté.
Dans une base de données commerciale, calculer le CA moyen des journées ensoleillées qui sont un lundi et dont la température est inférieure à 18°C.
L'utilisation de filtres permet d'extraire les fiches de la base de données correspondant aux critères.
L'utilisation des fonctions de bases de données permet également de résoudre une partie de ces problèmes.
Mais le calcul matriciel est de portée plus large, et ne nécessite généralement pas d'ajout de cellules supplémentaires (zones d'extraction, zones de critères…).
Le principe est simple. Le calcul est basé sur le fait que 1*VRAI = 1 et 1*FAUX = 0.


Dans le tableau ci-dessus, le temps est indiqué dans la plage D7:D37.
La matrice {=D6:D37="soleil"} (en colonne I) va donc renvoyer une matrice contenant VRAI pour chaque jour de soleil, FAUX pour les autres.
Et la matrice {=1*(D6:D37="soleil")} (colonne J) va renvoyer 1 pour soleil et 0 sinon.
La somme des cellules de la colonne J sera donc égale au nombre de 1, c'est à dire au nombre de jours de soleil.
Il suffit donc d'écrire {=SOMME(1*(D6:D37="soleil"))} (formule matricielle) pour obtenir, sur une seule cellule de calcul, le nombre de jour de soleil.
De la même façon, la formule {=SOMME((D7:D37="soleil")*F7:F37)} va renvoyer le chiffre d'affaires des jours ensoleillés.
En effet, pour les jours de soleil, la matrice {=D6:D37="soleil"} renvoie VRAI,
et la matrice {=(D7:D37="soleil")*F7:F37} renvoie la valeur de la colonne F, c'est à dire le CA.
On peut ajouter autant de conditions que souhaité :
La somme des CA des lundis au soleil :
{=SOMME((D7:D37="soleil")*F7:F37*(JOURSEM(C7:C37)=2))}
Et le CA moyen des lundis au soleil :
{=SOMME((D7:D37="soleil")*F7:F37*(JOURSEM(C7:C37)=2))
/SOMME((D7:D37="soleil")*(JOURSEM(C7:C37)=2))}
(Attention à l'utilisation de la fonction MOYENNE qui prendrait en compte pour une valeur nulle les cellules ne répondant pas aux critères. Il vaut mieux faire la somme divisée par le nombre).
La somme des CA des lundis ensoleillés dont la température est inférieure à 10°C :
{=SOMME((D7:D37="soleil")*F7:F37*(JOURSEM(C7:C37)=2)*(E7:E37<10))}
 
 
Il est d'ailleurs plus simple d'utiliser des plages nommées ("temps" pour D7:D37, CA pour F7:F37…). la formule devient très facile à comprendre :
{=SOMME(CA*(temps="soleil")*(JOURSEM(date)=2)*(température<10)*(région="sud"))}
{=SOMME(CA*(temps="soleil")*((JOURSEM(date)=7)+(JOURSEM(date)=1)))} va donner le cumul des CA des jours de week-end ensoleillés (noter l'utilisation du signe + pour prendre en compte les samedis et les dimanches).
 
Autre exemple, le tableau ci-dessous, directement exporté de Datastream vers Excel, donne l'évolution du prix du film polyéthylène mois par mois depuis 1986.
Comment calculer les prix moyens annuels ?


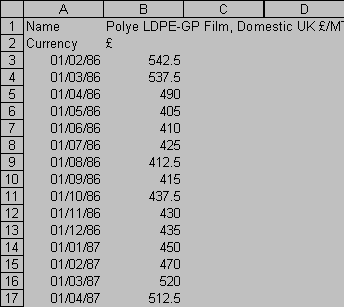
La matrice {=ANNEE(A3:A175)} donne l'année de chaque donnée.
La matrice {=ANNEE(A3:A175)=1990} donne donc VRAI pour toutes les données de 1990.
La somme des prix de 1990 s'écrit donc {=SOMME(B3:B175*(ANNEE(A3:A175)=1990))}
et le nombre de données de l'année 1990 {=SOMME(1*(ANNEE(A3:A175)=1990))}
d'où la moyenne
{=SOMME(B3:B175*(ANNEE(A3:A175)=1990))/SOMME(1*(ANNEE(A3:A175)=1990))}
Il suffit de construire un tableau avec en en-tête les années, et de remplacer 1990 par l'année :


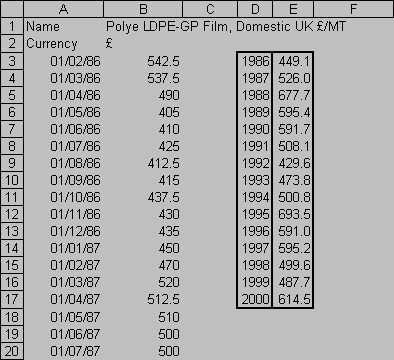
Formule en E3 :
{=SOMME(B$3:B$175*(ANNEE(A$3:A$175)=D3))/SOMME(1*(ANNEE(A$3:A$175)=D3))}
recopiée vers le bas jusqu'en E17.
 
 
On peut utiliser une formule matricielle pour comparer le contenu de deux plages de cellules :
la matrice {=A1:A7=B1:B7} est une matrice de 7 lignes sur une colonne contenant des VRAI dans les lignes pour lesquelles les valeurs saisies en colonnes A et B sont égales et FAUX dans les autres.
La formule matricielle (sur une cellule) {=ET(A1:A7=B1:B7)} renvoie donc VRAI si les deux plages A1:A7 et B1:B7 contiennent les mêmes valeurs, et FAUX sinon.



Pour la manipulation de matrices, on utilise souvents des matrices ne contenant que des 1 et des 0.
cliquez ici